

Mt. Everest, which straddles the border between China and Nepal, is the tallest mountain in the world. Measuring its height is no easy task and, in fact, the actual measurement has been a source of controversy for hundreds of years. The measurement process involves the use of triangles and a branch of mathematics known as trigonometry. In this section, we will define a new group of functions known as trigonometric functions, and find out how they can be used to measure heights, such as those of the tallest mountains.
We begin by drawing a circle centered at the origin with radius \(r\) , and marking the point on the circle indicated by some angle \(\theta\) as in Figure \(\PageIndex\) . This point has coordinates (\(x\), \(y\)). We can also say that (\(x\), \(y\)) is on the terminal side of angle \(\theta\).
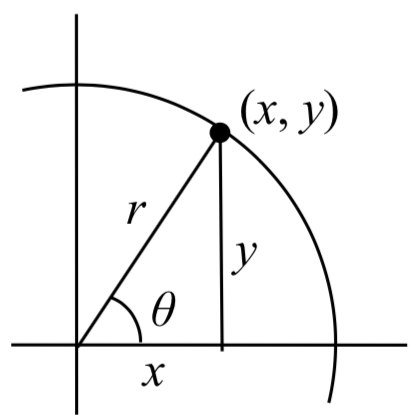
If we drop a line segment vertically down from this point to the x axis, we would form a right triangle inside of the circle.
No matter which quadrant our angle \(\theta\) puts us in we can draw a triangle by dropping a perpendicular line segment to the \(x\) axis, keeping in mind that the values of \(x\) and \(y\) may be positive or negative, depending on the quadrant.
Additionally, if the angle \(\theta\) puts us on an axis, we simply measure the radius as the \(x\) or \(y\) with the other value being 0, again ensuring we have appropriate signs on the coordinates based on the quadrant.
Triangles obtained from different radii will all be similar triangles, meaning corresponding sides scale proportionally. While the lengths of the sides may change, the ratios of the side lengths will always remain constant for any given angle.
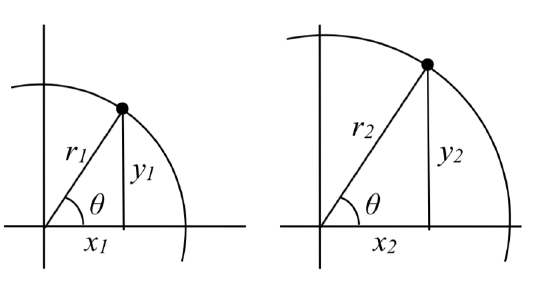
\(\dfrac > > =\dfrac > >\)
To be able to refer to these ratios more easily, we will give them names. Since the ratios depend on the angle, we will write them as functions of the angle \(\theta\).
The Six Trigonometric Functions
For the point (\(x\), \(y\)) on a circle of radius \(r\) at an angle of \(\theta\), we can define the six trigonometric functions as the ratios of the sides of the corresponding triangle:
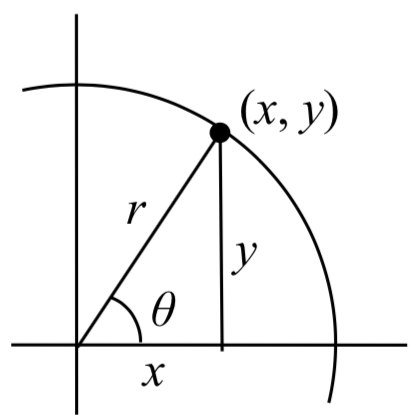
The sine function: \(\sin (\theta )=\dfrac\)
The cosine function: \(\cos (\theta )=\dfrac\)
The tangent function: \(\tan (\theta )=\dfrac\)
The cosecant function: \(\csc (\theta )=\dfrac\)
The secant function: \(\sec (\theta )=\dfrac\)
The cotangent function: \(\cot (\theta )=\dfrac\)
The point (3, 4) is on the circle of radius 5 at some angle \(\theta\). Find the six trigonometric function values of \(\theta\)
Solution
We have \(x=3\), \(y=4\), and \(r=5\). Using the previously listed definitions we have
\[ \sin (\theta )=\dfrac =\dfrac\\ \cos (\theta )=\dfrac =\dfrac\\ \tan (\theta )=\dfrac =\dfrac\\ \csc (\theta )=\dfrac =\dfrac\\ \sec (\theta )=\dfrac =\dfrac\\ \cot (\theta )=\dfrac =\dfrac \]
Consider once again the set-up with a right triangle inscribed in a circle with radius \(r\). The two legs of the right triangle are \(x\) and \(y\) and the hypotenuse is \(r\). According to the Pythagorean Theorem we have the following relationship:
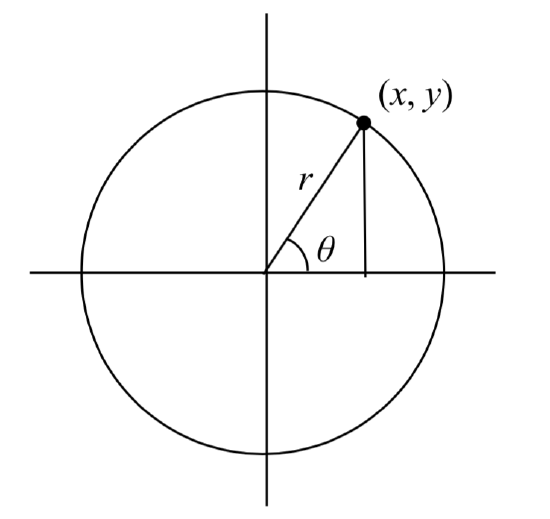
If we have a given point \( (x,y) \) on the terminal side of an angle, we can use the Pythagorean Theorem to find the length of the radius \(r\) and can then find the six trigonometric function values of the angle.
We now define the six trigonometric functions in terms of the names of the sides of a right triangle. First, let's recreate our right triangle (shown in Figure \(\PageIndex\). If we drop a vertical line segment from the point \((x,y)\) to the x-axis, we have a right triangle whose vertical side has length \(y\) and whose horizontal side has length \(x\). We can use this right triangle to redefine sine, cosine, and the other trigonometric functions as ratios of the sides of a right triangle.
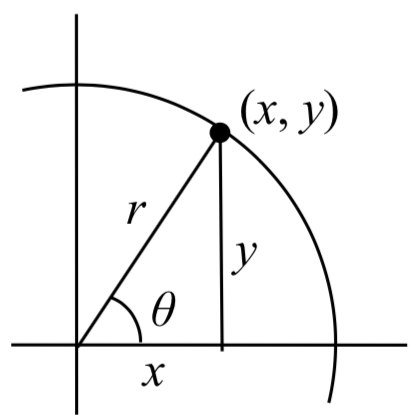
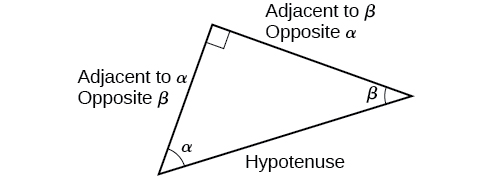
We want to have another way to express the ratios without relying on a set of axes. To be able to use these ratios freely, we will give the sides more general names: Instead of \(x\),we will call the side between the given angle and the right angle the adjacent side to angle \(\theta\). (Adjacent means “next to.”) Instead of \(y\),we will call the side most distant from the given angle the opposite side from angle \(\theta\). And instead of \(r\),we will call the side of a right triangle opposite the right angle the hypotenuse. These sides are labeled in Figure \(\PageIndex\).
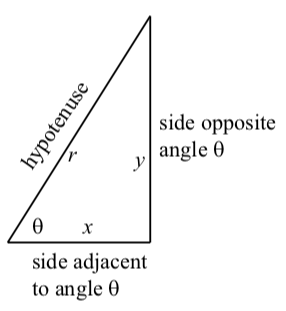
Given a right triangle with an acute angle of \(\theta\),
A common mnemonic for remembering these relationships is SohCahToa, formed from the first letters of “Sine is opposite over hypotenuse, Cosine is adjacent over hypotenuse, Tangent is opposite over adjacent.” To get the other three, we remember that cosecant is the reciprocal of sine, secant is the reciprocal of cosine, and cotangent is the reciprocal of tangent.
how to: Given the side lengths of a right triangle and one of the acute angles, find the sine, cosine, and tangent of that angle
Also remember that sine and cosecant are reciprocals, cosine and secant and reciprocals, and tangent and cotangent are reciprocals.
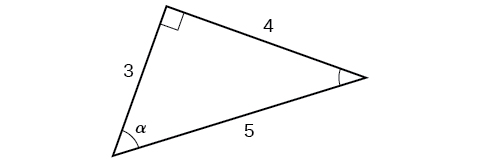
Example \(\PageIndex\): Evaluating a Trigonometric Function of a Right Triangle
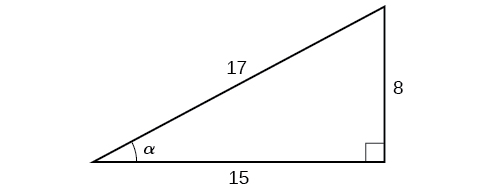
Given the triangle shown in Figure \(\PageIndex\), find the six trigonometric function values of angle \(\alpha\).
Solution
From the perspective of angle \(\alpha\), the adjacent side has length 15, the opposite side has length 8, and the hypotenuse has length 17, so we have
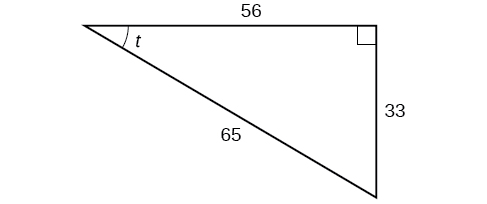
Given the triangle shown in Figure \(\PageIndex\), find the value of \(\sin t\).
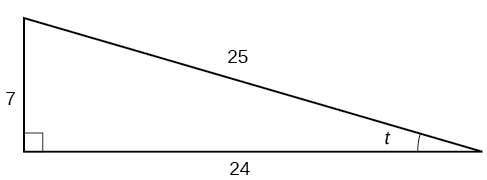
Answer
When working with right triangles, the same rules apply regardless of the orientation of the triangle. In fact, we can evaluate the six trigonometric functions of either of the two acute angles in the triangle in Figure \(\PageIndex\). The side opposite one acute angle is the side adjacent to the other acute angle, and vice versa.
We will be asked to find all six trigonometric functions for a given angle in a triangle. Our strategy is to find the sine, cosine, and tangent of the angles first. Then, we can find the other trigonometric functions easily because we know that the reciprocal of sine is cosecant, the reciprocal of cosine is secant, and the reciprocal of tangent is cotangent.
how to: Given the side lengths of a right triangle, evaluate the six trigonometric functions of one of the acute angles
Example \(\PageIndex\): Evaluating Trigonometric Functions of Angles Not in Standard Position
Using the triangle shown in Figure \(\PageIndex\), evaluate \( \sin α, \cos α, \tan α, \sec α, \csc α,\) and \( \cot α\).
Solution
Using the triangle shown in Figure \(\PageIndex\), evaluate \( \sin t, \cos t,\tan t, \sec t, \csc t,\) and \(\cot t\).
Answer
We now use our right triangle definitions to evaluate trigonometric values of special angles. We do this because when we evaluate the special angles in trigonometric functions, they have relatively friendly values, values that contain either no or just one square root in the ratio. Therefore, these are the angles often used in math and science problems. Our special angles are \(30°, 45°,\) and \(60°\)
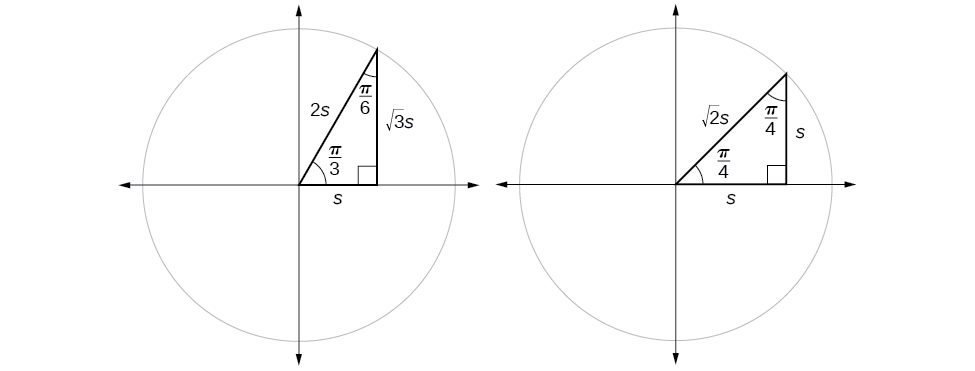
Recall from geometry the \(30°,60°,90°\) triangle, which can also be described as a \(\frac, \frac,\frac\) triangle. The sides have lengths in the relation \(s,\sqrts,2s.\) The sides of a \(45°,45°,90° \)triangle, which can also be described as a \(\frac,\frac,\frac\) triangle, have lengths in the relation \(s,s,\sqrts.\) These relations are shown in Figure \(\PageIndex\).
We can then use the ratios of the side lengths to evaluate trigonometric functions of special angles.
Given trigonometric functions of a special angle, evaluate using side lengths.
Example \(\PageIndex\): Evaluating Trigonometric Functions of Special Angles Using Side Lengths
Find the exact value of the trigonometric functions of \(\frac\), using side lengths.
Solution
Find the exact value of the trigonometric functions of \(\frac\) using side lengths.
Answer
If we look more closely at the relationship between the sine and cosine of the special angles relative to the unit circle, we will notice a pattern. In a right triangle with angles of \(\frac\) and \(\frac\), we see that the sine of \(\frac\), namely \(\frac<\sqrt>\), is also the cosine of \(\frac\), while the sine of \(\frac\), namely \(\frac,\) is also the cosine of \(\frac\) (Figure \(\PageIndex\)).
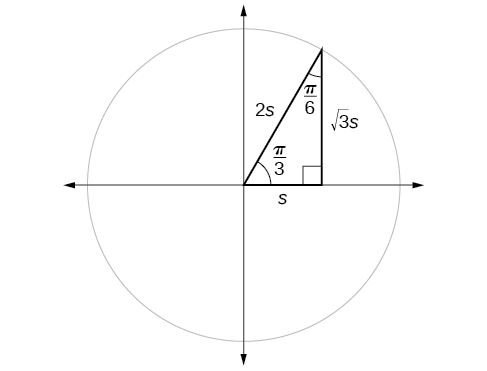
This result should not be surprising because, as we see from Figure \(\PageIndex\), the side opposite the angle of \(\frac\) is also the side adjacent to \(\frac\), so \(\sin (\frac)\) and \(\cos (\frac)\) are exactly the same ratio of the same two sides, \(\sqrt s\) and \(2s.\) Similarly, \( \cos (\frac)\) and \( \sin (\frac)\) are also the same ratio using the same two sides, \(s\) and \(2s\).
The interrelationship between the sines and cosines of \(\frac\) and \(\frac\) also holds for the two acute angles in any right triangle, since in every case, the ratio of the same two sides would constitute the sine of one angle and the cosine of the other. Since the three angles of a triangle add to π, π,and the right angle is \(\frac\), the remaining two angles must also add up to \(\frac\). That means that a right triangle can be formed with any two angles that add to \(\frac\)—in other words, any two complementary angles. So we may state a cofunction identity: If any two angles are complementary, the sine of one is the cosine of the other, and vice versa. This identity is illustrated in Figure \(\PageIndex\).
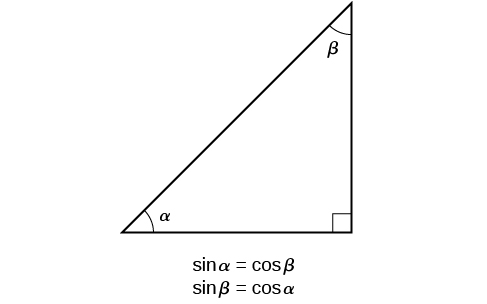
Using this identity, we can state without calculating, for instance, that the sine of \(\frac\) equals the cosine of \(\frac\), and that the sine of \(\frac\) equals the cosine of \(\frac\). We can also state that if, for a certain angle \(t, \cos t= \frac,\) then \( \sin (\frac−t)=\frac\) as well.
The cofunction identities in radians are listed in Table \(\PageIndex\).